From 3D to 2D with algebra

SEE THIS POST IN POLISH

To write a developing algorithm we need to get familiar with 2 topics from mathematical algebra .

3D coordinates and length of triangle sides

First we need to know all 3 sides of triangle .

A triangle can be defined with 3 points . And every point can be described with 3 coordinates (x,y,z) .

Distance between two points is equal to square root from sum of squared differences between point coordinates . See picture .

Construction

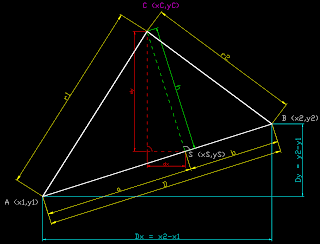
 Next step is made in 2 dimensions . First we define a line between two points A and B . distance between those points is equal to length of a first side of triangle ( D on a picture ) . Other sides of a triangle have lengths of  r₁ and  r₂ . We are looking for point C with coordinates (xC; yC) .

First step is to find point S .

From Pythagorean theorem for triangles ACS and BCS we:get :

r₁² = h² + a²

r₂² = h² + b²

From difference between those two equations :

r₁² - r₂² = a² - b²

r₁² -r₂² = (a+b) * (a-b)

And because D = a + b  and  b = D - a

r₁² -r₂² = D * (2a-D)

Therefore :

a = (r₁² -r₂² +D²) / 2D

Point S has coordinates :

xS = x₁ + (Dx * a) / D

yS = y₁ + (Dy * a) / D

When we know a we can also calculate h : h = √(r₁² - a²)

we can also write down two dependencies :

Dy / D = dx / h  =>  dx = - (Dy * h ) / D

( negative sign tells us that if Dy is positive(point B is above point A), then point C is to the left from point S and vice-verso )

Dx / D = dy / h  =>  dy = (Dx * h ) / D

Last step is getting coordinates of point C :

xC = xS + dx = x₁ + (Dx * a) / D - (Dy * h ) / D = x₁ + (Dx * a - Dy * h ) / D

yC = yS + dy = y₁ + (Dy * a) / D + (Dx * h ) / D = y₁ + (Dy * a + Dx * h ) / D

There is also second possible point C' that is situated below line AB

xC' = xS + dx = x₁ + (Dx * a) / D + (Dy * h ) / D = x₁ + (Dx * a + Dy * h ) / D

yC' = yS + dy = y₁ + (Dy * a) / D - (Dx * h ) / D = y₁ + (Dy * a - Dx * h ) / D

To be continued ...