Z 3D do 2D z algebrą

SEE THIS POST IN ENGLISH

Aby napisac algorytm który rozwinie nam powierzchnie, musimy zapoznac sie z dwoma zadaniami z matematyki .

W poprzednim etapie pokazywaliśmy jak Rozwinąc powierzchni przy pomocy geometrii wykreślnej , znając długosci bokow trójkąta .Teraz pokażemy jak dokonać tego przy pomocy liczb .

Współrzędne w przestrzeni 3D i długości boków trójkąta

Pierwszą rzeczą z którą musimy się zmierzyć jest długość boków trójkąta .
Trójkąt możemy zdefiniować w przestrzeni przy pomocy 3 punktów . A każdemu z tych punktów mozemy przypisać 3 współrzędne (x,y,z) .
Odległośc między punktami możemy zdefiniować jako pierwiastek z sumy kwadratów rożnic poszczególnych współrzednych .
W ten sposób mamy długości boków danego trójkąta .

Konstrucja

 Kolejny krok wykonujemy juz w przestrzeni dwuwymiarowej . Pierwszym etapem jest zdefiniowanie odcinka o dlugosci pierwszego boku ( D na rysunku ) . Odcinek ten zdefiniowany jest przez punky A i B i odpowiednich współrzędnych . Pozostale dwa boki trójkąta mają długośc odpowiedni r₁ i r₂ . Szukamy punktu C o współrzędnych (xC; yC) .

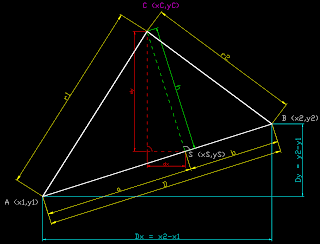
Pierwszym etapem jest znalezienie punktu S .
Rozpisując twierdzenie Pitagorasa dla trójkątów ACS i BCS otrzymujemy :
r₁² = h² + a²
r₂² = h² + b²
Z równań :
r₁² - r₂² = a² - b²
r₁² -r₂² = (a+b) * (a-b)
ponieważ D = a + b  i b = D - a
r₁² -r₂² = D * (2a-D)

stąd:
a = (r₁² -r₂² +D²) / 2D

Punkt S ma więc współrzędne:
xS = x₁ + (Dx * a) / D
yS = y₁ + (Dy * a) / D

Znając a możemy wyliczyć również h :  h = √(r₁² - a²)

Mozemy wypisać również następujące zależności :
Dy / D = dx / h  =>  dx = - (Dy * h ) / D
( znak mówi nam o tym że jeżeli Dy jest dodatnie, czyli punkt B jest wyżej niz punkt A, to punkt C znajduje się na lewo od punktu S i vice-versa )
Dx / D = dy / h  =>  dy = (Dx * h ) / D

Ostatni krok to wyznaczenie punktu C :
xC = xS + dx = x₁ + (Dx * a) / D - (Dy * h ) / D = x₁ + (Dx * a - Dy * h ) / D
yC = yS + dy = y₁ + (Dy * a) / D + (Dx * h ) / D = y₁ + (Dy * a + Dx * h ) / D

Jeżeli chcemy wyznaczyć analogiczny punkt C' który znajduje się poniżej odcinka AB :
xC' = xS + dx = x₁ + (Dx * a) / D + (Dy * h ) / D = x₁ + (Dx * a + Dy * h ) / D
yC' = yS + dy = y₁ + (Dy * a) / D - (Dx * h ) / D = y₁ + (Dy * a - Dx * h ) / D

C.D.N.